Sariel.pl

A complete tutorial on Lego gears, their advantages and disadvantages as well as the basic laws of mechanics that apply to them. Updated on February 19th 2010.

When I describe my constructions or ideas, and when I explain their functionality, I usually assume that readers have the basic understanding of mechanics and of the rules that apply to gears. This assumption, it seems, is sometimes wrong. Even though it may appear frustrating at times, I see no real reason to ignore the people who have not yet learnt how the gears work, nor to deny them the pleasure of building with Lego Technic. Having considered that, I prepared a document in which I’ve attempted to cover my entire knowledge on gears in an accessible manner. The tutorial you’re about to read should hopefully be useful both to beginners and to experienced builders. For better clarity it was divided into sections.

Contents:

1. Introduction to gears
2. Basic rules
3. Types of gears
4. Gear ratios
5. Efficiency
6. Backlash
7. Appendixes

1. Introduction to gears

What do we need gears for? A very usual answer is: to transfer the drive from a motor to the final mechanism. It is true, but not entirely correct. The essential purpose of gears is to transform the properties of a motor to suit our purposes in the best way possible. Transferring the drive is in fact a side-effect of this process.

Gears can be obviously used with all kinds of drive, be it an electric motor, a manual crank, a wind turbine, a mill wheel, whatever. For the purposes of this document we assume that drive is provided by an electric motor, because it’s a popular solution with Lego Technic, and one with constant properties that can be transformed with gears.

Every motor has its mechanical power, specific for a given type of motor. A number of types of Lego motor exists, some types offering greater power than the others. The important thing is that mechanical power of a motor consists of two factors: speed and torque. These are the two properties we can transform using gears.

Speed is simply the number of rotations of a driveshaft that the given motor produces within a given time interval. The higher the speed, the more rotations we get. In mechanics, speed is usually measured with RPM, that is Revolutions Per Minute. One RPM means one revolution of the motor’s driveshaft per minute – which is really slow. Most of the Lego motors offers more than 100 RPM.

Torque is the strength with which the driveshaft is rotated. The higher the torque, the more difficult it is to stop the driveshaft. Therefore motors which offer high torque are usually preferred to the other, because they can drive heavier vehicles or more complex mechanisms than the motors with low torque. The torque is measured in N.cm, and all we need to know is that the more N.cm, the stronger the motor.

The mechanical power is, in a certain simplification, the quotient of torque and speed. If we increase torque and/or speed, the mechanical power will be increased accordingly. In fact, the torque of a motor is constant – it can’t be changed without changing the motor’s construction. The speed, on the other hand, depends on the voltage at which the motor is powered. The higher the voltage, the higher the speed, which allows to increase the motor’s mechanical power by manipulating the voltage of its power supply. The official standard for Lego motors is 9V voltage, which is equal to the voltage of six AA batteries. The recently released Lego rechargeable battery provides 7.4V. It means that the motors powered from the battery have lower mechanical power than the ones powered from the AA batteries, but this is just a theory, because the voltage provided by the AA batteries decreases over time, and the voltage provided by the Lego battery remains more or less constant. Some experiments are done with motors powered at 12V, and though the motors produce higher mechanical power under these conditions, it should be noted that they were designed for 9V, not 12V, and it may result in a fatal damage to the motors. In this document we assume that all motors run at the same voltage, whether it’s 9V or less. You can find an exhaustive description of the performance of specific Lego motors here.

What do we need the speed and torque for? That is actually different for each mechanism. Consider a model of a sport car – we want it to be light and fast. It means that we certainly need large speed, but not the torque, because a light vehicle requires little torque to move. Using gears, we can transform torque into speed, or speed into torque. There are two very important, but very simple rules for that:

– if we drive a large gear with a small gear, we increase the torque but decrease the speed (that is called gearing down)
– if we drive a small gear with a large gear, we increase the speed but decrease the torque (that is called gearing up)

The best thing is that we can transform part of one property to increase the other, we don’t need to transform all of it. In the case of our sport car it means that we can pick a drive motor, and use the second of the aforementioned rules to gain extra speed at the cost of some needless torque. How much torque can we transform depends mainly on the car’s weight, so it’s a different value for every model. Experienced builders can estimate the range of possible transformation knowing just the vehicle’s weight and the type of the motor used to drive it. The basic rule is: speed and torque are inversely proportional. It means that if we decrease the speed twice, the torque is increased twice.

A different example would be a rail crossing barrier. We can raise or lower it with motor, but the nominal speed of any motor will be probably too large. A barrier should take at least several seconds to be fully raised or lowered, and most of the Lego motors run at more than 100 RPM. We need to use gears to get rid of this needless speed, and in exchange for that we will get extra torque, which can be used to operate a longer and heavier barrier. In this case, we use the first of the aforementioned rules.

Now that we know what gears can do, let’s have some theory.

2. Basic rules

In the first section we have learned the two rules of transferring torque into speed or speed into torque. We know what to use the gears for, and now we will learn how to use them. We will need a number of notions for that.

We can talk about using gears to transform motor’s properties when there are no less that two gears meshed, each set on a separate axle. The gear that is closest to the motor is called a driver gear. The gear that receives the drive from it is called a follower gear. On the diagram below the driver and follower gear are marked green and red respectively.

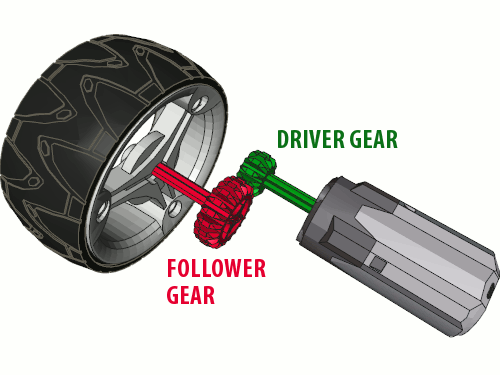
Almost every mechanism has its driver and follower gear. In every pair of meshed gears there is a driver gear and a follower gear. It should be sufficient to remember that the driver gear is the one the drive is transferred from, and the follower gear is the one the drive is transferred to.

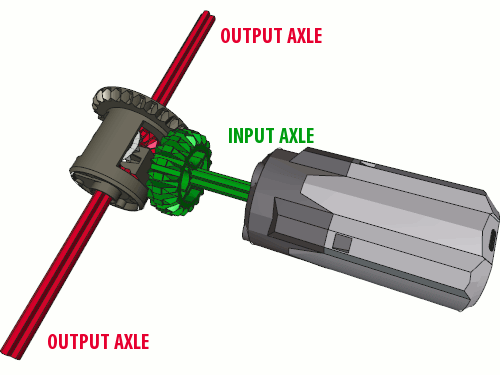
As you may have noticed, on the diagram above axles are marked with the same colours as the gears. That is because we can talk about axles in the same manner in which we have just described the gears. In fact, many mechanisms have covered or hidden gears but clearly visible axles, so this approach is often more convenient. In this case we call the axle with the driver gear (green) an input axle, and the axle with the follower gear (red) an output axle. That’s it: input and output, just like the driver and follower. Most of the mechanisms have usually a single input axle (because it’s difficult to drive many input axles with a single motor), but there are multiple output axles possible. The popular differential mechanism is a good example of one input / many outputs solution:

It doesn’t end just with the driver gear and follower gear: we have also an idler gear. If there is a number of gears meshed one by one, then only the first one is the driver gear and only the last one is the follower gear. All the gears in between are called idler gears, and that’s because they could as well not exist. Their presence does not affect how the torque and speed are transformed: only driver and follower gear determine that.

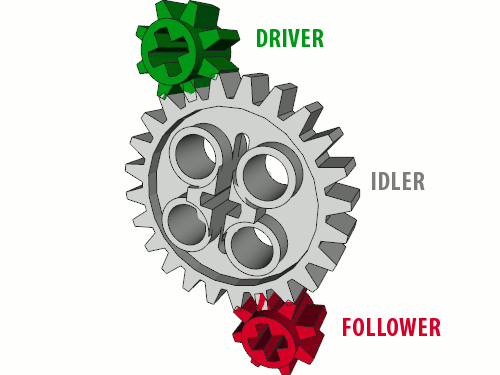
On the diagram above the large gray gear is meshed with driver gear at one side and with follower gear at the other. This is typical for idler gears: being meshed with many gears at the same time. Idler gears are usually meshed with two gears at the same time, while the driver and follower gear are only meshed with one. This is an easy way to identify the idler gears, but there are exceptions.

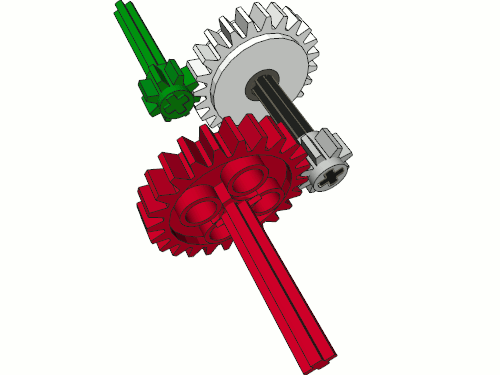
The diagram above shows two sets of gears. The left set contains a driver gear, a follower gear and two gears in between, each meshed with a single gear only. These two gears are set on the same axle, which means that they can be idler gears (not possible if they had separate axles), and they are of the same size, which means that they surely are idler gears. That is because many gears of the same size set on the same axle always act like a single gear – no matter whether there are 2 gears or 200. The right set also contains a driver gear, a follower gear and two gears in between, except these two gears are of different size. If they have different sizes while sharing the same single axle, they can’t be idler gears. That is because the difference in their sizes affects how the torque and speed are transformed between the driver gear and the follower gear. More precisely, the size of a gear affects the torque it transfers – we see that the gears share the same single axle, so their speeds must be equal, but their sizes are clearly different.

With this classification in mind, we can now have an exact look at the types of Lego gears.

3. Types of gears

Lego has released plenty of various types of gears in the history of Technic line. Below is the list of the ones that are still in use:

As you can see there are 13 classic, round gears, and there is one special gear called a worm gear. Moreover, the round gears can be divided into two groups: the regular ones with square teeth, and the bevel ones with rounded teeth. Practically any gear of the first group can be used with any gear of the second group. The unique property of the bevel gears is that they can be meshed in both parallel and perpendicular manner. They are also more convenient to use with liftarms because of their size. However, they are not suitable for use with the Lego chain.

Let’s have a short description of each gear on the list (bevel gears have the word bevel in their names):

8 teeth gear – the smallest gear currently being produced, and a very fragile one. It’s not suited for high torque, but very popular, especially for gearing down (being the smallest, it is obviously the most efficient at it). There are at least three different variants of this gear, and the most sought for one is reinforced by extra layer of plastic around the axle, between the teeth.

12 teeth gear (a single bevel one) –  the smallest bevel gear currently being produced. It’s not really useful for gearing down or up, but irreplaceable with differential mechanisms and very popular when there is a need to transfer the drive in a perpendicular manner inside a limited space. Easily broken under high torque, which led to complete absence of differentials in e.g. some trial trucks.

12 teeth gear (a double bevel one) – the smallest double bevel gear currently being produced. It’s much stronger than its single bevel counterpart, and is most usually used together with a 20 teeth double bevel gear.

14 teeth gear – the predecessor of the 12 teeth single bevel gear. It was the first gear designed specifically for differential mechanisms, but proved so very fragile that it was later replaced by the 12 teeth version. It is no longer used in the official Lego models and is unpopular with builders.

16 teeth gear (a regular one) – a reasonably strong and useful gear. This is the smallest gear that can be operated with Lego chain, and a popular one thanks to its convenient size. As of 2011, there is a new version of the 16 teeth gear available – see appendix B for details.

16 teeth gear (with clutch) –  available almost exclusively in dark gray, a gear designed specifically for gearboxes. It’s weaker than the regular version and doesn’t work well with Lego chain (it has a tendency to slip on it because of shorter teeth). Instead, it has the unique ability to be engaged or disengaged by the transmission driving ring. Without the ring, it remains loose on the axle, but it can be meshed with an old-type halfbush (the one with teeth) and thus get fixed to the axle.

20 teeth gear (a single bevel one) – larger version of the 12 teeth single bevel gear. Rare and not really popular because of its thin body which makes it snap under high torque.  Usually meshed with a 12 teeth double bevel gear or 20 teeth double bevel gear.

20 teeth gear (a double bevel one) – very popular, strong and reliable gear. Most commonly used together with a 12 teeth bevel gear, but useful in different setups too.

24 teeth gear (a regular one) – another popular, strong and reliable gear. There are at least three different variants of this gear, the newest ones being the strongest ones. One of the most useful gears ever.

24 teeth gear (with clutch) – a specific version of the 24 teeth gear, not related to the 16 teeth gear with clutch. It’s always white and dark gray in the middle, and it has the unique ability to harmlessly slip around the axle if a sufficiently high torque is applied. It makes it a very useful and sought for gear, although a rare one. Most usually it is used for end-to-end applications, that is applications when motor can only run until it reaches a certain point. This includes for instance almost all steering mechanisms, where the wheels can be turned only by a limited angle, or the aforementioned railroad barrier mechanism, where the barrier can be only raised or lowered to some degree. In this type of mechanisms this gear slips when that end point is reached, so that the motor can continue to run while the mechanism is stopped. Another example are winches in the official Lego sets with motorized winches (e.g. 8297), where this gear is used to make sure that motor doesn’t get damaged when the end of winch’s string is reached. Please note that this gear slips under a very specific amount of torque – and in most cases you will want it to slip only under extremely high torque (e.g. to make sure that the steering mechanisms stops turning when the end point is reached, not when a wheel meets an obstacle). This can be achieved by using this gear right after the driver gear:

Thanks to Jetro de Château it is confirmed that there have been at least three versions of this gear released over the years (photo courtesy of Jetro de Château):

From left to right, these are:
– version that came with the 8479 set, it has a light gray center and require more torque to slip
– version that is most commonly used, with dark gray center
– version from an unknown set(s), with smooth sides (no clutch power indications)

24 teeth gear (with crown) –  a really old design, the first gear among the regular gears which could be meshed in a perpendicular manner. Again, there are at least three variants of this gear, the older and weaker ones gradually replaced with never and stronger versions. The arrival of bevel gears made it one of the currently most unpopular gears; it’s weak and inconvenient to use. Still, it can be sometimes useful due to it’s unusual shape.

Worm gear – a gear with a number of unique properties. Firstly, it can be only used as the driver gear, never as the follower gear. It comes in handy for mechanisms that need to e.g. lift something up and keep it lifted; in this case worm gear acts like a lock that keeps the desired part of mechanism lifted without putting its load on the motor. There is a lot of possible applications for this worm gear’s property, for instance many types of cranes or forklifts, railroad barriers, drawbridges, winches, and basically every mechanism that needs to keep something steady once the motor stops.

Secondly, the worm gear is extremely efficient for gearing down. It is theoretically 8 times more efficient that the 8 teeth gear, because every revolution of the worm gear rotates the follower gear by just a single teeth. Therefore worm gears are used for gearing down whenever there is a very high torque or low speed needed and there is little space to use.

Finally, as the worm gear rotates, it has a tendency to push against the follower gear and slide along its own axle. Usually this tendency has to be stopped by a strong casing around the worm gear, but there are certain mechanisms that use it to move worm gear from one place to another, for instance my pneumatic autovalve or my automated trafficators system.

The worm gear can be used with all the listed gears. The most common use is to mesh it with a 24 teeth gear:

But it can be easily used with any other gear. You can see some examples of worm gears enclosed with follower gears inside strong casings here. With proper spacing, it can be used with bevel gears too:

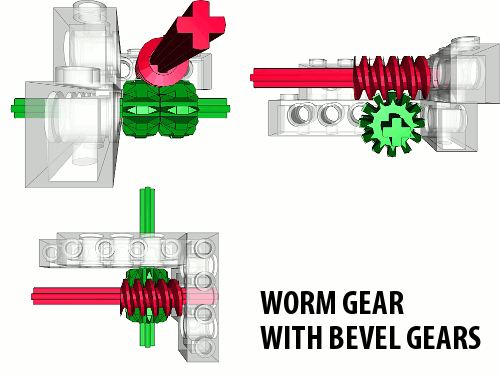
On the diagram above, there are two 12 teeth double bevel gears used. But it can be just a single double bevel gear, or two single bevel gears, or even a single single bevel gear. It’s even possible to use the worm gear to drive racks, which may result in e.g. a very compact boom extending mechanism:

36 teeth gear (a double bevel one) – the largest bevel gear currently being produced, and the only one with no single bevel counterpart. A convenient and surprisingly strong gear, but a rare one. Usually comes in black.

40 teeth gear (a regular one) – the largest regular gear currently being produced. Rarely used because of its immense size, but sometimes really useful.

That concludes the list of gears we can usually choose from (there are some outdated gears, but they are so unique that I actually never had any in my hands). Now let’s see why the sizes of gears matter.

4. Gear ratios

According to Wikipedia, the gear ratio is the relationship between the number of teeth on two gears that are meshed or two sprockets connected with a common roller chain, or the circumferences of two pulleys connected with a drive belt. We will not deal with pulleys in this document, and the ratios for sprockets connected with a common chain are exactly the same as for the gears that are directly meshed. Hence a gear ratio is simply:

number of follower’s gear teeth : number of driver’s gear teeth

Since the spacings between each gear’s teeth are equal, counting the number of teeth is a simple mean of calculating the gear’s circumference. And gear ratio is basically the relationship between gears’ circumferences.

What do we need the gear ratio for? Basically to easily calculate the final speed of the mechanism and the torque it provides. Consider an 8 teeth driver gear and 24 teeth follower gear. We know from the section 1 that this is gearing down: we gain some torque, but we loose some speed. The gear ratio is 24:8, which is equal to 3:1. Please note that it is a common practice to calculate ratios in such a manner that they end with 1. Why? Because from looking at 3:1 ratio we can easily tell that it means that the revolution’s speed is reduced three times, which means that three revolutions of the driver gear / input axle result in a single revolution of the follower gear / output axle. Since the decrease of speed results in an inversely proportional increase of torque, we know that torque is increased three times.

Consider an opposite example: we have a 20 teeth driver gear and 12 teeth follower gear. The gear ratio is 12:20, which is equal to 0.6:1. It means that we need 0.6 revolution of the driver gear to get a single revolution of the follower gear. Hence we gain 40% of speed, but we lose 40% of torque.

As you could have noticed, it is easy to tell gearing up from gearing down looking at the gear ratio. If the first number of the gear ratio is greater than the second (like 3:1), this is gearing down – also called a gear reduction. If the first number of the gear ratio is smaller than the second (like 0.6:1), this is gearing up – also called a gear acceleration or an overdrive. If we have 1:1 gear ratio, speed and torque remain the same, just as if we used idler gears.

We can already calculate gear ratios of two meshed gears, but what if there are more gears in the mechanism? In this case, we ignore all the idler gears and calculate ratios for all pairs of driver/follower gears. Then, in order to get the final gear ratio of the entire mechanism, we simply multiply these gear ratios. Consider a mechanism from section 3, with two pairs of 8 teeth drivers and 24 teeth followers. The gear ratio of the first pair is 3:1, and so is the ratio of the second pair. If we multiply these ratios, we get the final ratio equal to 9:1 – which is true and accurate.

Now that we can calculate gear ratios, let’s go back to the example of idler and non-idler gear from section 2:

Consider the left set of gears. It consists of two pairs of gears: 8 teeth driver gear with 16 teeth follower, and 16 teeth driver with a 20 teeth follower (let’s assume we don’t know if there are idlers in this set yet; we calculate ratio of each pair separately). The ratio of first pair is 2:1, and the ratio of second pair is 1.25:1. If we multiply these, we get the final ratio equal to 2.5:1. 2.5:1 is equal to 20:8 – that is the ratio of the first and the last gear only. As you see, the idler gears did not change the ratio at all, and this is why we can ignore them.

Now consider the right set of gears. It consists of another two pairs of gears: 8 teeth driver gear with 16 teeth follower gear, and 24 teeth driver gear with 20 teeth follower gear. The ratio of first pair is again 2:1, but the ratio of the second pair is  0.833:1. If we mutliply these, we get the final ratio equal to 1.66:1 – which is not equal to 2.5:1 (the ratio of the first and the last gear only). Here the middle gears were not idlers, so they affected the final gear ratio of the whole set and they couldn’t be ingnored.

Finally, how do we calculate ratio if a worm gear is used? Well, that’s even simplier:

number of follower’s gear teeth : 1

And that’s  because as it was mentioned before, a single revolution of a worm gear rotates the follower gear by a single teeth. Therefore it takes 24 revolutions of the worm gear to rotate a 24 teeth gear once, and hence we get the ratio 24:1 which is true.

You can use this calculator to calculate the ratios of your Lego mechanisms.

5. Efficiency

We had some theory, now we need to get back to practice, which is unfortunately a bit sad. Every gear we use has some weight and generates some friction that has to be overcome if we want the gear to rotate. Hence every gear in our mechanism uses part of the drive motor’s power, and efficiency of the gear tells us how much power is transferred and how much is lost. Unfortunately, it’s extremely difficult to calculate individual efficiency of each gear, and as far as I know there are no reliable specifications for the efficiency of Lego gears. But we know how the power is lost, so we can safely assume two basic rules for maximum efficiency:

– the less gears, the better
– the smaller gears, the better

Sadly, it means that e.g. gear ratio equal to 1:1 is only theoretical. If there are gears, there are losses, so the real ratio has to be 1.something:1. The only mechanism in which the 1:1 ratio is possible is a motor connected directly to the final gear – for example in my model of Leclerc T6 tank, the drive motors were connected directly to the wheels in order to achieve 1:1 efficiency.

What about gear acceleration? Yes, you can obviously use gears to get e.g. 1:6 gear ratio which will greatly increase your speed. However,  the quotient of your final speed and torque will be smaller than the quotient of the motor’s original speed and torque – because of the losses. Using gears always includes losses, therefore if you want to transform the speed and torque of a motor, you have to keep in mind that some of it will be lost.

There are two cases  of mechanisms in which the efficiency is crucial. First is a gearbox with transmission driving rings. This type of a gearbox uses a number of 16 teeth gears with clutch, and while all of these gears are driven, only some of them transfer the actual drive. It means some of these gears – majority of them, if the gearbox has more than 4 speeds – use motor’s power for nothing. They are so-called dead gears, which is even worse than idler gears because idler gears are usually needed to transfer the drive from one place to another, while the dead gears are not needed at all. And they can’t be removed from such a gearbox, because every gear selected uses a different set of gears to transform the drive. It means that a certain gear can work as a dead gear at 1st, 2nd and 3rd gear, but is needed to transform the drive at the 4th gear. A gearbox with many dead gears always performs better at lower gears, when there is a large gear reduction – it makes the drive motor use little of its power to actually do its primary task, so it has plenty of power to drive the dead gears. You can see from the video of my 10-speed manual gearbox that motor becomes more and more strained as gears are shifted from 1st to 2nd, then to 3rd and so on. In fact, some time after this gearbox was published I have built a 14-speed version, just out of curiosity. When I connected it to a PF XL motor, it was stalled and could not drive the gearbox even at the 1st gear despite it’s excellent torque.

The second mechanism is… a worm gear. As mentioned before, a worm gear is popular because it offers an extremely high gear reduction. But this is actually the worst gear in terms of efficiency – some sources estimate that it loses almost one third of the motor’s power due to high friction (friction is the very reason why worm gear can’t be a follower gear) and its tendency to slide along its axle. The friction is high enough to make worm gears hot if they handle high torque for a prolonged period of time. Worm gears are irreplaceable for some applications, but in general they should be only used when necessary.

6. Backlash

Gear tooth backlash is generally a complex issue (more at Wikipedia). For the purpose of Lego mechanics we can simply assume that backlash is the free space between the meshed teeth of two adjacent gears. In a perfect situation there should be no free space at all, and the teeth should have full contact with each other. This situation is unfortunately very difficult to achieve with standard gears (it’s much easier with helical gears, but these are absent in the Lego Technic world), and Lego gears always generate some backlash. The general rules are:

– regular gears generate much greater backlash than the bevel ones
– the smaller the gear, the greater the backlash
– the backlashes of any two meshed gears sum up

You can easily guess that 8 teeth gear is a real dynamite when it comes to generating backlash. Out of all regular gears, the 40 teeth one generates the smallest backlash. Among the bevel gears, differences are much smaller due to a different teeth design – any bevel gear generates a backlash several times smaller than in case of the feared 8 teeth gear. As pointed out above, the backlashes of meshed gears sum up, therefore it’s a good idea to use regular gears together with the bevel gears – the resulting backlash will be somewhat reduced.

How does it work for a worm gear? Again, this gear proves unique generating practically no backlash. It doesn’t mean that mechanisms with the worm gear have zero backlash – unfortunately, they still have backlash of the follower gear. Therefore a mechanism with a worm gear and a 16 teeth follower gear will always have greater backlash than the one with a worm gear and a 24 teeth follower gear. And again, it is recommended to use worm gear with bevel gears due to their relatively insignificant backlash.

Why is backlash bad? Consider a steering mechanism with big wheels, driven by a motor reduced 27 times – which means that three pairs of an 8 teeth driver gear and 24 teeth follower gear have been used. Three 8 teeth gears together generate a backlash so large that it will not only degrade the accuracy of steering – it will also make the steered wheels have some margin of freedom, so that they can e.g. turn a bit when they meet an obstacle.

Backlash is usually not a real problem for vehicles (except for the very large ones), but it’s troublesome whenever accuracy is needed. Many sorts of e.g. cranes, drawbridges or turntables suffer from backlash. The best way to avoid it is to consider the use of pneumatics instead of mechanics, or the use of linear actuators which currently have the least backlash out of all the mechanical parts produced by Lego.

I hope you have found this tutorial useful, and that it helped you to enjoy the Lego Technic world a little more.

7. Appendixes

Appendix A: gear 20 teeth bevel with pin hole, knob wheel, and differences between three 8t gear types

In 2010 a new type of gear was introduced: the gear 20 teeth bevel with a pin hole. It was, as you can easily see, a modification of the earlier gear 20 teeth bevel intended to offer some new possibilities, not to replace it. These possibilities are most obvious with linear actuators: the problem with actuators is that when they are attached to an axle using the articulated bracing, they sit on the same axle that drives them. It means that the load on an actuator generates friction on the axle that drives it, and it results in its efficiency degrading rapidly as the load increases.

The new gear appears to be designed specifically to solve this issue. So far it was possible to transfer drive to an actuator in such a setup using gear 12 teeth single bevel or gear 20 teeth single bevel – now we have a third option. The difference is, the new gear rotates freely around the axle, so it can be used as an idler gear without the need to actually rotate the axle it sits on. Therefore the load on the linear actuator no longer affects the efficiency of gears that drive it. This picture illustrates the three set-ups, with the new gear being the third one (please note that all three set-ups offer 1:1 gear ratio):

The new gear is also thicker, thanks to a half-stud thick collar at its base. The earlier 20 teeth single bevel gears have been known to easily snap under torque because they had only a limited contact with the axle, and the collar in the new gear helps greatly. The new gears are much less likely to snap, and their only disadvantage is that because of their pin hole, they can only be used as idler gears.

The knob wheels have been around for a couple of years – they were omitted from the tutorial earlier because technically they’re not a gear wheels. There are two important things to know about the knob wheels: firstly, they only mesh with another knob wheels, and secondly, they are much stronger than gear wheels and they can handle significantly higher torque. The latter property makes them popular among e.g. the Truck Trial builders. Knob wheels can be meshed both in perpendicular and parallel manner. They are most commonly used in the perpendicular set-up, because the regular gears that can transfer the drive in such a set-up are much more likely to snap under torque than the knob wheels. A good example of the knob wheels’ usage is the 8421 LEGO set, where they were used to operate transverse outriggers, with a significant torque involved. The disadvantage of the knob wheels is that for the most of the time they are only meshed at one point (two points in the parallel set-up), and that this point changes four times per a single rotation. Therefore they work like a gear with only 4 teeth, that is: they work unevenly. It is particularly apparent when a large torque is applied to a perpendicular set-up of knob wheels – their speed of rotation starts to fluctuate. Also, because of having all the torque applied to so few points, the knob wheels are prone to wearing out. It is a common thing in the Truck Trial vehicles to see the knob wheels rub away at their meshing points – but it only happens with really heavy vehicles and only after a while.

Finally, the three types of 8 teeth gears that were mentioned in the tutorial. LEGO is known to make small modifications to its molds over time, and many LEGO parts have slightly changed their shape over years. It’s difficult to sort out the chronological order of changes affecting the 8 teeth gears, but it seems that the strongest version was introduced as the last one and is commonly used in the recent Technic sets. Please note that this is just a supposition: there’s a chance that several variants of the same parts are still produced from various molds, and that a specific set may contain one type or the other, or even a mix of types. The gears, however, look like this:

The gear on the left seems to be the initial variant of the 8 teeth gear. The middle gear, that was introduced some time later, has the same central part but a different shape of the teeth: they are shorter and thicker, and presumably stronger. This is a minor difference, hard to notice until you put two variants of this gear together. The third gear represents the apparently ‘current’ variant. It maintains the shape of the teeth introduced in the middle variant, but its central part has an apparent extra layer of material between the teeth, adding to its thickness. This is quite a noticeable difference, and is probably intended to prevent the teeth from bending under torque. This variant of the gear is most sought-for by any builder aware of these differences.

Appendix B: the new version of the 16 teeth gear

As of  early 2011, the classic 16 teeth gear has been modified. The version we have known before is apparently being gradually replaced with a new version coming from a slightly different mould:

The picture above shows the old version on the left (part number 4019) and the new version on the right (part number 94925). As you can see, the shape of the gear’s outer rim is exactly the same, whereas the structure in the middle of it has been significantly altered. It appears that the new version is supposed to be stronger and less prone to mechanical damage from high torque, as its centre is clearly more massive. Additionally, the outer ring around the gear appears roughly twice as thick, which is most likely another factor that makes the new version of the gear more torque-resistant.